Một điều kỳ diệu vừa xảy ra với bóng đá Anh, không phải là trận thua của Arsenal trước Paris Saint-Germain ở bán kết lượt đi UEFA Champions League đêm qua, mà là chức vô địch Premier League sớm 4 vòng đấu của Liverpool, đã được ấn định vào chủ nhật tuần trước.
Sau khi đánh bại thuyết phục Tottenham Hotspur với tỷ số 5-1 trên thánh địa Anfield, cộng với việc Arsenal, đội đứng thứ hai ở Premier League bị Crystal Palace cầm hòa 2 đều, Liverpool đã bỏ xa Arsenal tới 15 điểm, trong khi giải đấu chỉ còn 4 vòng cuối.
Điều đó đồng nghĩa với việc họ đã chính thức lên vô địch Giải Ngoại hạng.

Tin tức này có vẻ đến chậm trễ, nhưng hãy khoan, chính các nhà toán học cũng phải mất tới 3 ngày để phát hiện ra điều kỳ diệu đằng sau chức vô địch của Liverpool năm nay: Nó đã hoàn thành trọn vẹn một dãy số Fibonacci trong toán học, trên bảng thống kê thành tích vô địch Giải Ngoại hạng của các câu lạc bộ tại Anh.
Cụ thể, từ khi Premier League bắt đầu khởi tranh vào năm 1992, đã có 7 câu lạc bộ nâng cao chiếc cúp của giải đấu này. Trong đó, áp đảo là Manchester United với 13 chức vô địch, kế tiếp là đội bóng cùng thành phố Manchester City với 8 chức vô địch.
Chelsea có 5 chức vô địch. Con số của các câu lạc bộ Arsenal, Liverpool, Leicester City và Blackburn Rovers lần lượt là 3, 2, 1, 1.

Khi xếp các con số này ngược lại, các nhà toán học đã giật mình, vì nó chính là dãy Fibonacci: 1, 1, 2, 3, 5, 8, 13… Có vẻ như chức vô địch của Liverpool năm nay là một tín hiệu của vũ trụ, bởi ngoài họ thì việc Leicester City và Blackburn Rovers vô địch Ngoại hạng là không thể.
Trong trường hợp có bất kỳ một sự xáo trộn nào xảy ra, ví dụ như Arsenal, đội đã liên tiếp về nhì 3 mùa giải gần đây của Ngoại Hạng Anh, lên ngôi, hoặc Manchester United vô địch thêm một mùa giải bất kỳ từ năm 2013 tới nay, dãy Fibonacci cũng sẽ biến mất.
Nhưng tại sao dãy số này lại đặc biệt đến vậy với toán học?
Với những người chưa biết, Fibonacci là một chuỗi số mà mỗi số là tổng của hai số trước đó: 0+1=1, 1+1=2, 2+1=3, 3+5=8, 5+8=13… và kéo dài đến vô cực. Điều khiến các nhà toán học mê mẩn dãy số này là nó tồn tại như một tỷ lệ vàng trong tự nhiên.
Dãy số này được các nhà thơ, và có lẽ cũng là nhà toán học Ấn Độ thời trung cổ, phát hiện khi nghiên cứu mô hình trong thơ ca tiếng Phạn. Cụ thể, họ muốn tìm cách tổ chức các âm tiết dài (guru ứng với 2 nhịp thời gian) và ngắn (laghu ứng với 1 nhịp thời gian) trong các khổ thơ, để tạo ra nhịp điệu hài hòa như thể một bài hát.
Các nhà thơ Ấn Độ tự hỏi: Với một số nhịp nhất định, có bao nhiêu cách để sắp xếp các chữ có âm tiết ngắn và dài? Ví dụ:
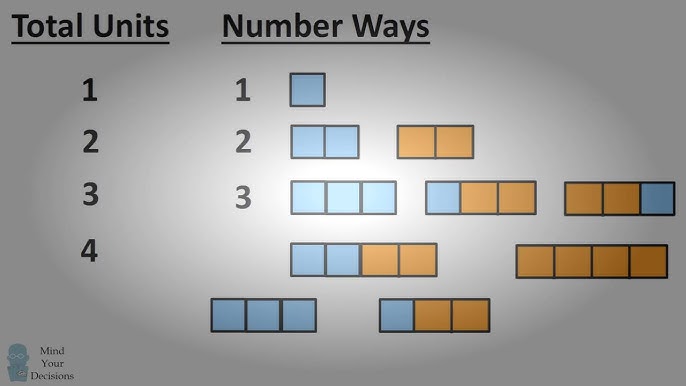
Các âm tiết dài guru màu cam ứng với 2 nhịp thời gian và ngắn laghu màu xanh ứng với 1 nhịp thời gian.
– Với 1 nhịp: Chỉ có 1 cách sắp xếp 1 tâm tiết ngắn
– Với 2 nhịp: Có 2 cách (2 âm tiết ngắn hoặc 1 âm tiết dài)
– Với 3 nhịp: Có 3 cách (3 ngắn, hoặc 1 dài + 1 ngắn, hoặc 1 ngắn + 1 dài)
– Với 4 nhịp: Có 5 cách (4 ngắn, hoặc các kết hợp khác như dài + ngắn + ngắn, ngắn + dài + ngắn…)
Cứ thế, khi số nhịp tăng dần, số cách kết hợp các âm tiết của bài thơ sẽ tăng theo đúng dãy Fibonacci.
Tuy nhiên, các học giả Ấn Độ không phải là người đặt tên cho dãy số này, mà đó là Leonardo Bonacci, một nhà toán học người Ý.

Nhà toán học người Ý Leonardo Bonacci, người đặt tên dãy Fibonacci.
Vào năm 1202, khi Bonacci quan sát lũ thỏ sinh sản, ông đã nghĩ rằng mỗi cặp thỏ phải sinh ra được một cặp thỏ khác sau mỗi tháng.
Nếu vậy, bắt đầu với một cặp, số lượng thỏ sẽ tăng theo dãy 1, 2, 4, 8, 16, 32, 64, 128…, tức nhân đôi mỗi tháng. Nhưng thực tế lại không như vậy.
Bonacci nhận ra thỏ cần một chu kỳ để trưởng thành về mặt sinh sản. Do đó, từ một cặp thỏ, số lượng tăng chậm hơn: 1, 1, 2, 3, 5, 8, 13, 21, 34… Mỗi số là tổng của hai số trước.
Vì nhận thấy tính chất của nó quá đẹp, ông đã ghi lại dãy số đặc biệt này, đặt tên nó là Fibonacci xuất phát từ cụm từ tiếng Ý “filius Bonacci”, dịch ra nghĩa là “con trai của dòng họ Bonacci”.
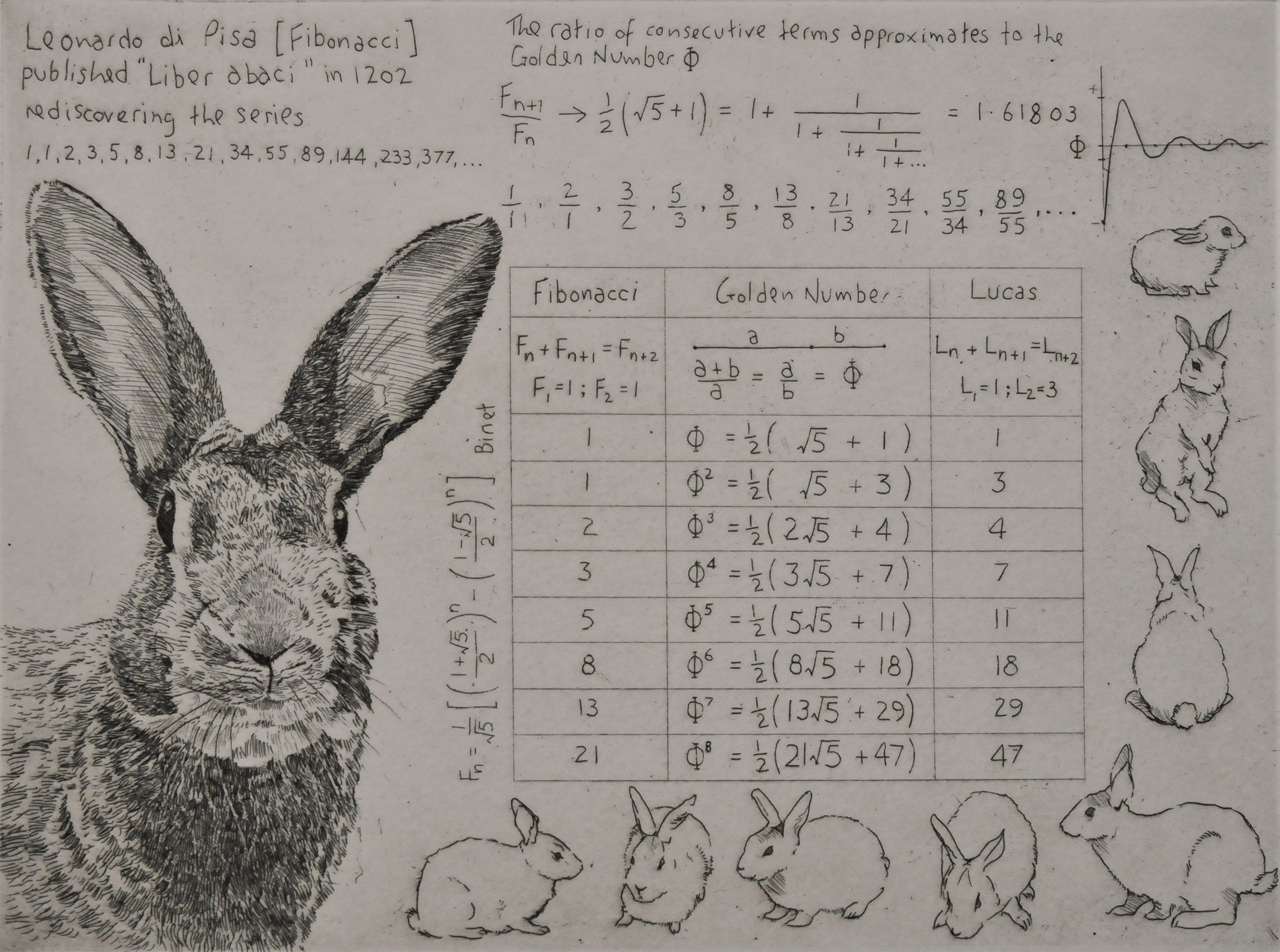
Điều kỳ diệu của dãy Fibonacci
Sau khi Bonacci phát hiện ra dãy Fibonacci, nó đã thu hút một loạt các nhà toán học Châu Âu lao vào tìm hiểu nó. Và khi càng tìm hiểu, họ càng nhận thấy đây là một dãy số kỳ diệu.
Fibonacci xuất hiện gần như ở mọi nơi trong tự nhiên, “nhảy” cả vào những lĩnh vực tưởng chừng không liên quan đến toán học. Chẳng hạn, cách sắp xếp các nụ hoa súp lơ, nhụy hoa hướng dương, hoa văn trên vỏ ốc đều tăng theo dãy Fibonacci.
Dãy Fibonacci còn gắn liền với “tỷ lệ Vàng” φ (phi) có giá trị khoảng 1,618. Bởi càng tiến lên trong dãy số, khi lấy số liền sau chia cho số liền trước, bạn sẽ được những con số tiến tới tỷ lệ vàng từ cả hai chiều.
Ví dụ, 5 chia 3 bằng 1,66, lớn hơn φ một chút. 8 chia 5 bằng 1,6, nhỏ hơn φ một chút. 13 chia 8 bằng 1,625, lại lớn hơn φ một chút nhưng đã tiến gần đến φ hơn 1,66. 21 chia 13 bằng 1,6154, lại nhỏ hơn φ một chút nhưng tiếp tục tiến gần hơn 1,6.
Nhưng tại sao Fibonacci và tỷ lệ vàng lại liên quan đến cây cỏ?
Bạn hãy nghĩ về lá cây. Năng lượng của cây đến từ ánh sáng mặt trời, nên cây cần tối ưu hóa vị trí lá để hấp thụ ánh sáng. Cách đơn giản là mỗi lá mới mọc lệch một góc so với lá trước, nhưng lệch bao nhiêu thì hợp lý? Nếu mọc lệch một nửa vòng, lá thứ ba sẽ chồng lên lá đầu tiên, che mất ánh sáng. Tương tự với các góc như 1/3 hay 1/4 vòng.
Giải pháp là chọn một góc ‘vô tỷ’, và góc vô tỷ nhất chính là góc liên quan đến Tỷ lệ Vàng. Cách tiếp cận thực tế nhất để đạt được góc này là sử dụng các số Fibonacci.
Điều tương tự cũng xảy ra với những thực thể khác trong tự nhiên, từ vỏ ốc, hạt hướng dương cho đến bông súp lơ.




Những tỷ lệ vàng này xuất hiện nhiều trong tự nhiên đến nỗi chúng trở thành một thứ gì đó rất hài hòa và thuận mắt với con người. Các họa sĩ thời kỳ Phục Hưng như Leonardo da Vinci đã thường xuyên áp dụng nó vào tranh vẽ và các tác phẩm của mình.
Một cách kỳ diệu thay, tòa nhà Parthenon ở Hy Lạp hay kim tự tháp Giza ở Ai Cập cũng có kích thước tuân theo tỷ lệ vàng, mà không rõ các kiến trúc sư cổ đại có cố tình áp dụng nó hay không.
Ngay cả trong âm nhạc, nhịp điệu hay cấu trúc của một số bản giao hưởng cũng phản ánh dãy Fibonacci. Dãy số này giống như một “mật mã” của vũ trụ, và bây giờ, nó đã xuất hiện trong giải Ngoại hạng Anh.
Điều đó có nghĩa là gì?
Một số giả định có thể đựa đưa ra. Chẳng hạn, có người cho rằng sự xuất hiện của dãy Fibonacci thể hiện Premier League bằng cách nào đó đang tự tối ưu hóa nó.
Cách nguồn lực, tiền đầu tư cho các câu lạc bộ đang được phân bổ theo tỷ lệ vàng, điều đó dẫn đến khoảng cách về trình độ của các đội bóng đang tuân thủ theo đúng dãy Fibonacci kéo theo xác suất vô địch của họ.
Hoặc cũng có thể có thuyết âm mưu nói rằng các nhà cái đã can thiệp vào Giải Ngoại hạng và sự can thiệp của họ vô tình đã tạo ra tỷ lệ vàng.

Tuy nhiên, tất cả những lời giải thích này nghe có vẻ hơi miễn cưỡng. Các nhà toán học cho rằng nhiều khi, dãy Fibonacci chỉ xuất hiện một cách vô tình và nó chỉ khiến chúng ta chú ý đến nó hơn mà thôi.
“Mặc dù có nhiều hình xoắn ốc xuất hiện từ các quá trình vật lý thuần túy, phi sinh học trong tự nhiên – từ các xoáy nước và dòng xoáy hình thành trong các khối nước, đến hình dạng trên không của các đám mây bão – nhưng không có hình xoắn ốc nào trong số này giống Fibonacci một cách hoàn hảo khi nhìn vào chi tiết toán học và cấu trúc bền vững của chúng trong thực tế “, nhà vật lý thiên văn Ethan Siegel nhận định.
“Bạn có thể chụp nhanh một tấm ảnh, trong đó, một hoặc nhiều đặc điểm của vật thể đúng với tỷ lệ của chuỗi Fibonacci. Nhưng cấu trúc đó của vật thể sẽ không tồn tại lâu dài và bền vững, mà chỉ xuất hiện trong một khoảnh khắc tại một thời điểm cụ thể mà thôi”.


Số lượng chức vô địch của các câu lạc bộ Manchester United, Manchester City, Chelsea, Arsenal, Liverpool, Leicester City và Blackburn Rovers đang tạo thành chuỗi Fibonacci hoàn hảo như tranh vẽ.
Điều đó có nghĩa là một con ốc anh vũ có các đường xoắn Fibonacci vào ngày hôm nay, nhưng tới ngày mai, vỏ ốc của nó sẽ khác đi một chút và phá vỡ tỷ lệ vàng đó. Tương tự với những bông súp lơ, hạt hướng dương và kế hoạch sinh đẻ của lũ thỏ.
Giải Ngoại hạng Anh cũng vậy. Nếu bất kỳ đội bóng hàng đầu nào trong số 7 đội đã giành chức vô địch Premier League tiếp tục vô địch vào năm sau, chuỗi Fibonacci sẽ bị phá hỏng. Chúng ta sẽ phải đợi rất lâu để bước tiếp theo của chuỗi Fibonacci xuất hiện trở lại.
Chẳng hạn như Manchester City phải vô địch thêm 5 mùa giải. Song song với đó, Chelsea vô địch thêm 3 mùa, Arsenal thêm 2 mùa, Liverpool thêm 1 mùa. Leicester City và Blackburn Rovers một trong 2 đội vô địch thêm 1 mùa.
Phải có một đội hoàn toàn mới lần đầu vô địch. Và quan trọng nhất, đội đang có thành tích tốt nhất trên dãy Fibonacci, Manchester United phải vô địch thêm 8 mùa giải nữa để đạt tới con số 21 chức vô địch.

Lần gần nhất Manchester United vô địch Premier League là mùa giải 2012-2013
Điều đó rõ ràng chẳng dễ dàng gì khi Manchester United đã trải qua 12 mùa giải không có danh hiệu Premier League. Năm nay, họ còn đang đứng ở vị trí thứ 14 trên bảng xếp hạng và vừa nhận tin chắc chắn không xuống hạng vào tuần trước.
Mặc dù vậy, cũng phải công nhận một thực tế, nếu đội bóng giàu thành tích nhất Ngoại hạng Anh không sa sút đến vậy, có lẽ chúng ta sẽ chẳng bao giờ được chứng kiến dãy Fibonacci xuất hiện ở Giải Ngoại hạng Anh.
Có lẽ, ban huấn luyện Manchester United cũng rất yêu toán học, hoặc đơn giản, vũ trụ đã ra những tín hiệu ngẫu nhiên, mách bảo họ phải làm như vậy.
Nguồn tin: https://genk.vn/cac-nha-toan-hoc-giat-minh-phat-hien-liverpool-vo-dich-arsenal-ve-nhi-lien-tiep-3-mua-giai-manchester-united-that-bai-suot-12-nam-la-de-hoan-thanh-day-fibonacci-o-giai-ngoai-hang-anh-2025043018521924.chn